3. daļa

1. uzdevums

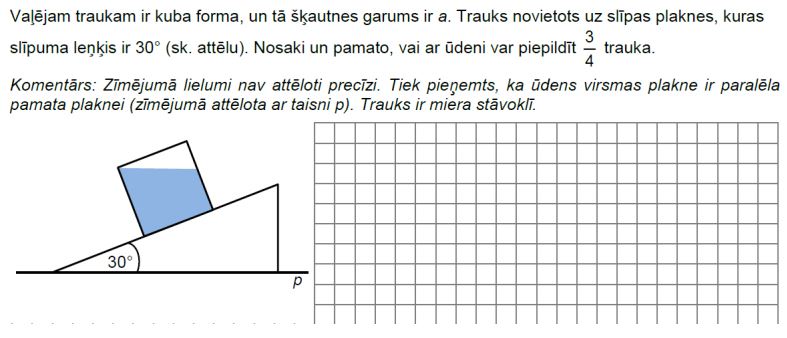
a – kvadrāta malas garums

b – baltā trijstūra īsākās malas garums

Pirmkārt, var izrēķināt baltā trijstūra laukumu.

No baltā trijstūra:

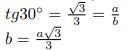
Tātad baltā trijstūra laukums ir 

Lai traukā varētu ieliet šķidruma, nepieciešams, ka baltais trijstūris nepārsniedz 25% no kvadrāta kopējā laukuma

tas jāpierāda ( vai jāapgāž)

Vienādosim saucējus:

Tātad jānoskaidro, vai 

Zināms, ka   Tātad, lai izpildītos nevienādība,  vērtībai jābūt ne lielākai par 1.5, bet tā nav taisnība, līdz ar to atbilde ir skaidra – traukā nevarēs ieliet  ūdens.

2. uzdevums

Vispirms tiek iegūta virkne: 4, 12, 24, 40…
No tā secinu par vispārējo formulu: an = 2(n2 + n).
Tātad 10×10 kvadrātam tiks izmantoti: a10 = 2(102 + 10) = 2 · 110 = 220 sērkociņi.
Lai iegūtu lielāko iespējamo režģi, ko var uztaisīt no 400 sērkociņiem:

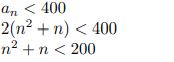
Var atrisināt kvadrātnevienādību:

 (neder)

 (der)

Atbilde – ar 400 kociņiem varēs izveidot 13×13 lielu režģi.

3. uzdevums

Nosaki vienādojuma  sakņu skaitu visām parametra n vērtībām, ja n ir vesels, no nulles atšķirīgs skaitlis.

Risinājums:

Izšķir 3 gadījumus:

a) 

b) 

c) 

b) Ja , tad iegūstam x = x, tātad bezgalīgi daudz sakņu.
c) Ja , tad vienādojuma kreisā puse ir pakāpes funkcija, bet labā puse – lineāra funkcija (kas iet caur 0 punktu, iet caur 1.un 3.kvadrantu). Zināms, ka
pakāpes funkcijas izskats atkarīgs no pakāpes, tāpēc izšķirsim vēl 2 gadījumus:

• n – pāra
• n – nepāra.
Ja n – pāra, tad pakāpes funkcijai atrodas 1. un 2.kvadrantā, tātad, lineārā
funkcija to krusto 2 reizes. Vienu reizi koordinātu krustpunktā, un otro reizi
1.kvadrantā.
Ja n – nepāra, tad pakāpes funkcija atrodas 1. un 3.kvadrantā,  tātad, lineārā
funkcija to krusto 3 reizes. Vienu reizi koordinātu krustpunktā, otro reizi 1.kvadrantā, un 3. reizi 3.kvadrantā

a) Ja 

Veidojas līdzīga situācija kā c gadījumā , izšķir to,  kāds daļskaitlis veidojas.
Tad kreisajā pusē veidojas saknes funkcija, kuras grafiks atkarīgs no kāpinātāja
saucēja. Pieņemot, ka  seko, ka

Tātad, ja b – pāra, veidojas 2 krustpunkti, jo saknes funkcija atrodas tikai
1.kvadrantā, un lineāro funkciju krusto 2 reizes – 0 punktā un 1.kvadrantā.
Ja b-nepāra, veidojas 3 krustpunkti, jo saknes funkcija atrodas 1. un 3.kvadrantā. Lineāro funkciju krusto 3 reizes: katrā no kvadrantiem, kurā atrodas un
0 punktā .