7. uzdevums

Risinājums:

No pirmās rindiņas:

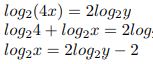
No otrās rindiņas:

Tā kā kreisās puses vienādas, tad arī labajām vienādojumu pusēm jābūt vienādām.

 no tā seko, ka 

Ievietojiet y vietā tikko atrasto vērtību:

 no tā seko, ka 

Atbilde: (16;8)

---

 

8. uzdevums 

Students no 21 ir iemācījies 16 jautājumus. Zināms, ka eksāmenā tiks iekļauti 2 no 21 jautājuma. Aprēķini varbūtību, ka students ir iemācijies:

a) abus iekļautos jautājumus;

b) vismaz vienu no iekļautajiem jautājumiem.

Risinājums: Varbūtība, ka viens no jautājumiem ir tāds, ko students ir iemācījies ir  Lai abus iekļautos jautājumus students būtu iemācījies, jāzina arī varbūtība, ka otrais jautājums ir studenta zināms.

Tāda varbūtība ir  jo palikuši 20 jautājumi, un no atlikušajiem students zina 15.

Tātad a) gadījumā: 

b) gadījumā jāizrēķina varbūtība, ka viens jautājums ir zināms, bet otrs ne.

Tā kā tika prasīta varbūtība VISMAZ vienam no jautājumiem, tad a) gadījumā iegūtā varbūtība jāsaskaita ar tikko iegūto:

---

---

 

9. uzdevums 

No uzdevuma nosacījumiem skaidrs, ka gan attālums l, gan laiks t, kurā abi sasniedz galamērķi B, ir vienādi.

Ar x apzīmēsim pirmā sportista ātrumu (km/h).

Tātad, no fizikas kursa 

Tāpēc iespējams izteikt 

Pēc mums zināmās informācijas, spēkā ir šādi nosacījumi:

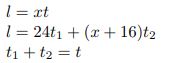
Ar  un  tiek apzīmēts atbilstoši laiks, cik ilgi 2. sportists brauca ar ātrumu 24 km/h, un cik ilgi ar ātrumu x+16 km/h.

Tā kā visiem šiem nosacījumiem jāizpildās reizē, var izveidot vienādojumu:

Tātad 

Zināms, ka 

Ievietojot iepriekš iegūtajā vienādojumā:

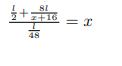
Šis vienādojums jāatrisina:

Sāksim ar lielāko daļu:

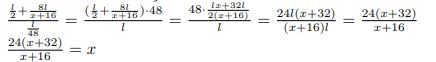
Abas puses pareizina ar x + 16

Atrisinot šo kvadrātvienādojumu iegūst divas saknes:

x = -24 (neder, jo ātrums nevar būt negatīvs)

x = 32, kas arī ir atbilde uz uzdevumu jautājumu.

---

 

10. uzdevums

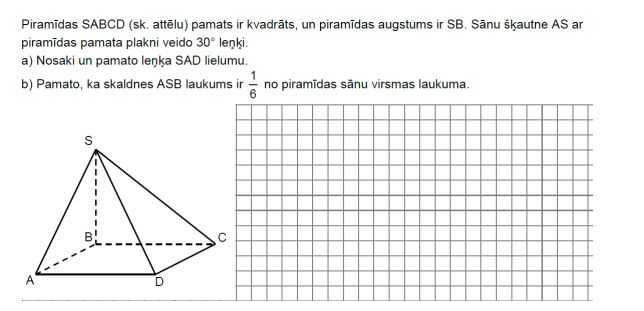
a) Leņķis SAD ir 90 grādu liels, jo tā šķautnes AS projekcija ir AB, kas ir kvadrāta mala.

b) Pirmkārt, varam novērot, ka trijstūri SAB un SBC ir vienādi savā starpā, tāpat kā SAD un SDC.

Turpmāk kvadrāta malas garums apzīmēts ar burtu a. No trijstūra SAB:

Tā kā leņķis SAB ir 30 grādu, tad

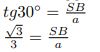
No šejienes: 

Tātad trijstūru SAB un SBC laukumu var aprēķināt reizinot kateti ar kateti un dalot ar 2, šajā gadījumā SB un kvadrāta malu.

Lai iegūtu piramīdas sānu virsmas laukumu, jāizrēķina arī trijstūru SAD un SDC laukumi.

No trijstūra SAB var iegūt malu SA:

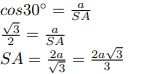
Līdz ar to, var aprēķināt trijstūru SAD un SDC laukumus:

Tagad var iegūt sānu virsmas laukumu:

Un ir redzams, ka trijstūra SAB laukums ir 6 reizes mazāks nekā piramīdas sānu virsmas laukums.