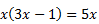atveram iekavas
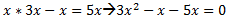Tā kā būs kvadrātvienādojums, tad labajā pusē jābūt 0.
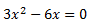Savelkam līdzīgos, redzams, ka tas ir nepilnais kvadrātvienādojums. Risina, iznesot kopīgo pirms iekavām.
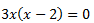Iekavu reizinājums ir nulle, ja kāds no reizinātājiem ir nulle. Pielīdzinām nullei abus reizinātājus.
- 3x = 0 no šejienes seko, ka pirmā sakne
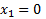
- x – 2 = 0 Pārnesot skaitļus labajā pusē seko, ka otrā sakne
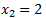Atbilde. Vienādojuma saknes ir 0 un 2
Jāsāk ar to, ka jāaprēķina katra saskaitāmā vērtība:
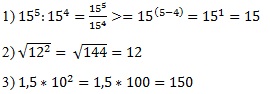
Tālāk jāizpilda aritmētiskās darbības kā uzdevumā: 15 + 12 – 150 = -123
2.1 Izmantoto reizināšanas paņēmienu (detektīvromānu skaits) x (autobiogrāfisko romānu skaits) 3 x 4= 12
2.2 Varbūtība ir izsakāma kā šāda daļa:
Tātad šajā gadījumā 
2.3 Izmantoto reizināšanas paņēmienu (romānu skaits)x(romānu skaits -1) = 20 x 19 = 380(k.)
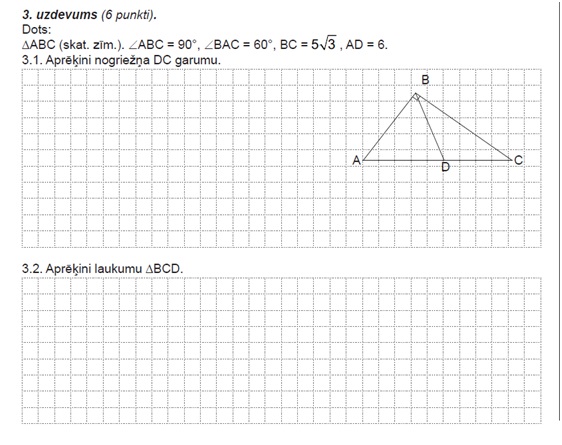
3.1 Tā kā ABC ir taisnleņķa trijstūris, aprēķinām leņķi ACB. Tas ir 30 grādu. (180-90-60) Tad izmantojot trigonometrisko sakarību sinuss leņķim ACB: 
Tagad zināms AC garums, varam atņemt AD garumu, un būsim ieguvuši DC: 
3.2 Trijstūra laukuma aprēķināšanai izmantosim formulu: 
Mūsu gadījumā a ir BC, b ir DC un y ir ACB leņķis. Ievietojam: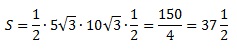 
Lai atrisinātu nevienādību sistēmu, aprēķina katru nevienādību atsevišķi un skatās kopīgo daļu.:
1.nevienādība
13(1 – x) > 39 atver iekavas
13 – 13x > 39 x vienā pusē, skaitļi otrā
-13x > 39 – 13 izpilda darbību labajā pusē, apgriež nevienādību uz otru pusi
13x > -26 abas puses izdala ar 13
x > -2 iegūts atrisinājums x > -2
2.nevienādība
labajā pusē atstāj nulli, pārējo uz kreiso pusi
vienādo saucējus
izpilda atņemšanu
savelk līdzīgos
izdara secinājumus par daļas zīmi:
Tagad saucēju var atmest, zinot, ka tas ir pozitīvs. Seko, ka x – 1 < 0 – – > x < 1
Tagad skatās kopīgo atrisinājumu: x < 1 un x > -2 Atbilde: 
5.1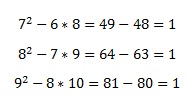 
5.2 Trīs pēc kārtas secīgus naturālos skaitļus var uzrakstīt šādi:
