3.DAĻA

1.uzdevums
Salīdzini izteiksmjuvērtības, ja a ∈ (-∞ ; 0) U (0; +∞) . Aplūko visus iespējamos gadījumus.

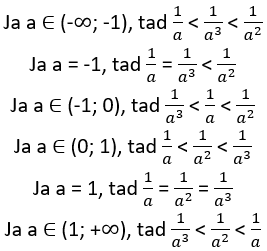
2.uzdevums
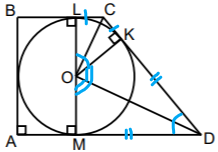
Taisnleņķa trapecē ABCD ievilkta riņķa līnija ar centru punktā O. Trapeces malas BC, CD, AD pieskaras riņķa līnijai attiecīgi punktos L, K, M (skat. att.). Pierādi, ka
a) LC + MD = CD,
b) ∠LOK = ∠KDM,
c) ∠COD = 90°.

a) pēc pieskares īpašības
LC = CK un MD = DK
tātad LC + MD = CK + DK = CD

b) leņķisLOK = x; tad tā blakusleņķis MOK = 180° – x

četrstūra KDMO leņķu summa ir 360°,

tādēļ leņķis MDK = 360° – (leņķis OMD + leņķis OKD + leņķis MOK) = 360° – (90° + 98° + 180° – x) = x

gan leņķis LOK, gan leņķis KDM ir vienādi ar x

c) trijstūris LOC = trijstūri KOC

OC – kopīga; LC = CK – pieskares; LO = OK – rādiusi => vienādos trijstūros atbilstošie leņķi ir vienādi

leņķis LOC = leņķi KOC

Tāpat pierāda, ka leņķis KOD = leņķi MOD

leņķis COK + leņķis KOD = 1/2 no leņķa LOM = 90°

3.uzdevums
a) Dots apgalvojums: bezgalīga virkne ir dilstoša. Nosaki un pamato, vai apgalvojums ir patiess.
b) Definē ar formulu bezgalīgu virkni, kurai piemīt divas īpašības: 1) virkne ir dilstoša; 2) virknes katrs loceklis ir lielāks nekā. Pamato virknes abas īpašības.