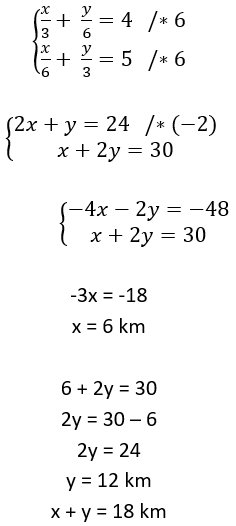2.DAĻA
1.uzdevums
Atrisini nevienādību 
.
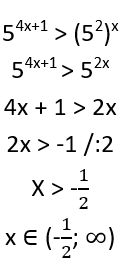
2.uzdevums
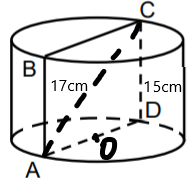
Cilindra (sk. att.) aksiālšķēluma ABCD diagonāles AC garums ir 17 cm, bet cilindra augstuma CD garums ir 15 cm. Aprēķini cilindra pilnas virsmas laukumu.
3.uzdevums
Atrisini vienādojumu 
.
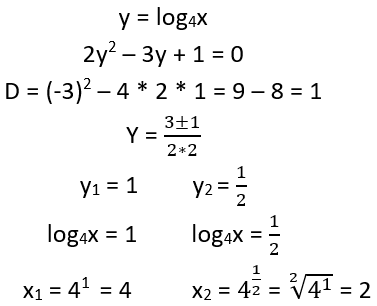
4.uzdevums
Dota izteiksme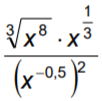
, kur x > 0. Pārveido doto izteiksmi par x pakāpi.
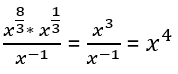
5.uzdevums
Dots funkcijas y = 2x + 8 grafiks (sk. att.).
a) Dotajā koordinātu plaknē uzzīmē arī funkcijas y = 
grafiku. Zīmējot grafiku, nosaki koordinātas vismaz četriem grafika punktiem un atliec tos.
b) Nosaki visus x, kuriem funkcijas y= vērtība ir lielāka nekā funkcijas y = 2x + 8 vērtība.
c) Nosaki visus x, kuriem abu funkciju (y = un y =2x + 8) vērtības ir pozitīvas.
d) Izmantojot funkciju grafikus, nosaki vienādojuma = 2x + 8sakni.
a)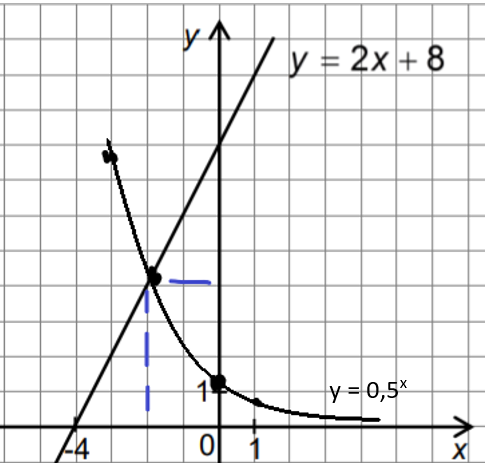 
b) x ∈ (∞; -2)
c) x ∈ (-4; ∞)
d) x = -2
6.uzdevums
Atrisini vienādojumu sin2x – sinx = 0.
2sinxcosx – sinx = 0
sinx (2cosx – 1) = 0
sinx = 0 2cosx – 1 = 0
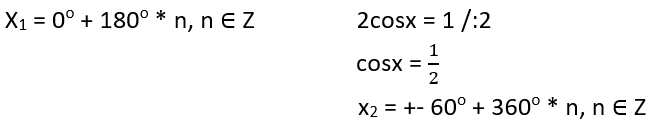
7.uzdevums
Veic uzdevuma tekstā aprakstītās konstrukcijas. Uzdevuma daļās b) un c) daudzpunktes vietā ieraksti konstruētās ģeometriskās figūras apzīmējumu, lietojot lielos burtus.
Dots kubs ABCDA1B1C1D1 (sk. att.). Punkts K pieder šķautnei DD1.
a) Konstruē punktu P, kurā taisne C1K krusto plakni ABC.
b) Konstruē taisni, pa kuru šķeļas plaknes C1KB un ABC.
Plaknes C1KB un ABC šķeļas pa taisni ……….. .
c) Konstruē kuba ABCDA1B1C1D1 šķēlumu ar plakni C1KB.
Kuba ABCDA1B1C1D1 šķēlums ar plakni C1KB ir daudzstūris ……………. .
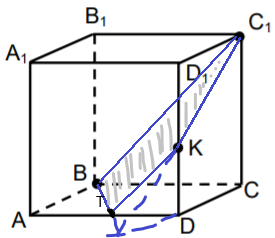
b) BP
c) BC1KT
8.uzdevums
Durvju kodu atslēgai ir 6 taustiņi – apzīmēti ar burtu simboliem A, B, C, D, E, F. Kodu var veidot no k dažādiem burtu simboliem (k iespējamās vērtības ir 1; 2; 3; 4; 5). Lai atvērtu durvis, uzstādītajam kodam atbilstošie taustiņi jānospiež vienlaicīgi.
a) Uzraksti visus dažādos kodus, ja k = 2 (ievēro – piemēram, AE un EA ir viens un tas pats kods).
b) Cik dažādu kodu var izveidot, ja k = 3?
c) Dots apgalvojums: jo lielāka k vērtība, jo lielāks izveidojamo kodu skaits. Nosaki un pamato apgalvojuma patiesumu.
a) AB; AC; AD; AE; AF; BC; BD; BE; BF; CD; CE; CF; DE; DF; EF
b) 
c) Apgalvojums nav patiess, jo, ja
k = 5, tad 
9.uzdevums
Trijstūra piramīdas SABC pamats ir vienādsānu trijstūris ABC (AB = BC). Piramīdas augstuma SO pamats O atrodas pamata augstuma BD viduspunktā.
a) Papildini piramīdas SABC zīmējumu atbilstoši dotajam aprakstam.
b) Nosaki un pamato, kura no piramīdas sānu šķautnēm ir īsākā.
c) Zināms, ka AC garums ir b, bet īsākās sānu šķautnes garums ir 2b un ar pamata plakni tā veido 45°. Aprēķini piramīdas tilpumu.
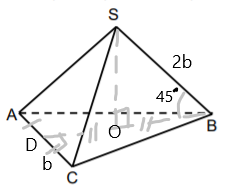
b) SB ir īsākā sānu šķautne, jo tās projekcijas
OB = OD < OC (trijstūrī OCD OD – katete; OC – hipotenūza)
OC ir SC projekcija
vai
OB = OD un OA ir attālums no O līdz AC, kas ir īsāks nekā OC.
c) 
10.uzdevums
Tūrists devās no kalnu ciemata A uz kalnu ciematu B un atgriezās atpakaļ ciematā A pa to pašu maršrutu. Maršruts sastāv no vairākiem ceļa posmiem, kas ved kalnup, un vairākiem posmiem, kas ved lejup (līdzenu ceļa posmu nav). Turpceļā tūrists pavadīja 4 h, bet atpakaļceļā 5 h. Visus ceļa posmus, kas ved kalnup, tūrists veica ar nemainīgu ātrumu 3 km/h. Visus ceļa posmus, kas ved lejup, tūrists veica ar nemainīgu ātrumu 6 km/h. Aprēķini attālumu starp kalnu ciematiem A un B.
x…tik kur ir kalnup, ceļā no A uz B
y…tik ir lejup, ceļā no A uz B
