2.veids. Ar Vjeta teorēmu.
Lai risinātu kvadrātvienādojumu ar Vjeta teorēmas palīdzību, nepieciešams, ka koeficients a=1.

Tad kvadrātvienādojums ir formā To sauc par reducēto kvadrātvienādojumu.

Vienādojuma saknes var atrast, atrisinot sistēmu:

Piemērs.

Liek iekšā sistēmā:

Tālāk jādomā, kuru divu skaitļu reizinājums dod 6 un summa 5.

Piebilde.

Konkrētas metodes, kā risināt šādu sistēmu, nav. Taču, ja vienādojuma saknes ir veseli skaitļi, tad diezgan viegli pārbaudīt visus veselo skaitļu reizinātājus, kas reizinot dod  koeficientu C . Ja saknes ir daļskaitļi, tad sakņu atrašanas process būs garš, tad tiek rekomendēts izmantot diskriminanta metodi .

Tāpat arī Vjeta teorēmas formulas nedod atbildi, ja dotajam vienādojumam sakņu nav – to var pārbaudīt tikai izrēķinot diskriminantu.

Atgriežoties pie piemēra – diezgan veikli var izspriest, ka reizinājumu 6 dod tikai 2 iespējas 1 un 6,    2 un 3.

1+6 nav 5 = > 2+3 =5 .

Saknes ir atrastas un tās ir 2 un 3.

Piemērs.

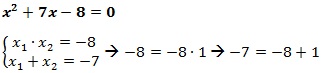
1.solī domāju, kuri divi veseli skaitļi dos nepieciešamo reizinājumu.

2.solī – vai to summa ir -b. Ja pārbaudot izpildās, tad vienādojuma saknes ir atrastas!

Atbilde.