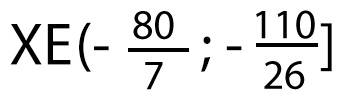Par nevienādību sistēmu sauc k nevienādības (), kurām jāatrod visi kopīgie atrisinājumi.
Piebilde. Kopīgi atrisinājumi var arī neeksistēt, tad saka, ka atrisinājumu kopa ir tukša kopa ().
Nevienādības iedalās stingrajās () un nestingrajās (). Nestingrās nevienādības lieto, ja nepieciešams ieskaitīt arī intervāla galapunktus. Tad lieto kvadrātveida iekavu – [ ].
Lai atrisinātu nevienādību sistēmu nepieciešams atrisināt katru nevienādību atsevišķi. Pēc tam visus atrisinājumus apvienot. Visērtāk to izdarīt izmantojot reālo skaitļu asi.
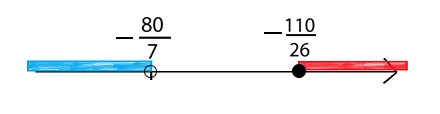
Piemērs:

Pirmās nevienādības atrisinājums attēlots ar sarkanu krāsu, bet otrās – ar zilu krāsu. Kopīgais atrisinājums . Tas arī jāraksta atbildē.
Atgādinājums!
Lai atrisinātu šādu nevienādību : jāatceras, ka abas nevienādības puses drīkst dalīt ar vienu un to pašu skaitli. Savukārt, ja skaitlis, ar ko dala ir negatīvs, tad nevienādības zīme mainās uz pretējo. Doto nevienādību dalot ar -3 iegūst

Nevienādību sistēmu var pierakstīt izmantojot ne tikai figūriekavu, kas ietver visas nevienādības. Alternatīvs nevienādību sistēmas uzdošanas veids ir dubultnevienādība.
Kā risināt Nevienādību sistēmas?
Lai atrisinātu šādi uzdotu nevienādību sistēmu, ērti ir pāriet uz jau pazīstamo veidu. Viss kas jādara – jāpārraksta katra nevienādība atsevišķā:
PIEMĒRS:
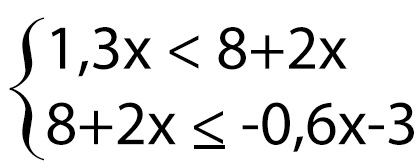
1. Darbība – pārnest X vienā pusē skaitļus otrā pusē
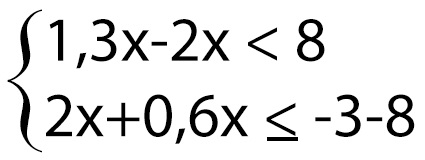
2. Darbība – saskaitīt/atņemt skaitļus, un izrēķināt cik ir X
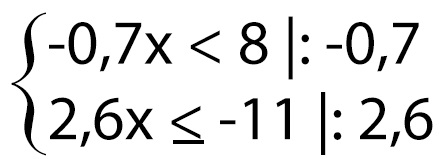
3. Darbība – pierakstīt pareizi
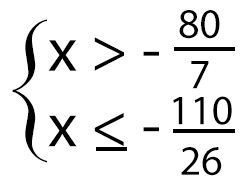
4. Darbība – pierakstīt pareizi atbildi