3.DAĻA

1.uzdevums
a) Nosaki visus reālo skaitļu pārus, kas ir vienādojuma (x – 1) * (y – 2) = 0 atrisinājumi. Rakstot atbildi, izvēlies sev piemērotāko veidu – pieraksti ar matemātiskiem simboliem vai apraksti vārdiski.
b) Koordinātu plaknē attēlo nevienādības (x – 1) * (y – 2) < 0 visu atrisinājumu kopu.
c) Uzraksti nevienādību, kuras atrisinājums ir visi tie skaitļu pāri, kuri nav nevienādības (x -1) * (y – 2) < 0 atrisinājumi.

a) (x – 1)(y – 2) = 0
x = 1          y = 2
x = 1  un   y ∈ R
y = 2  un   x ∈ R

b)

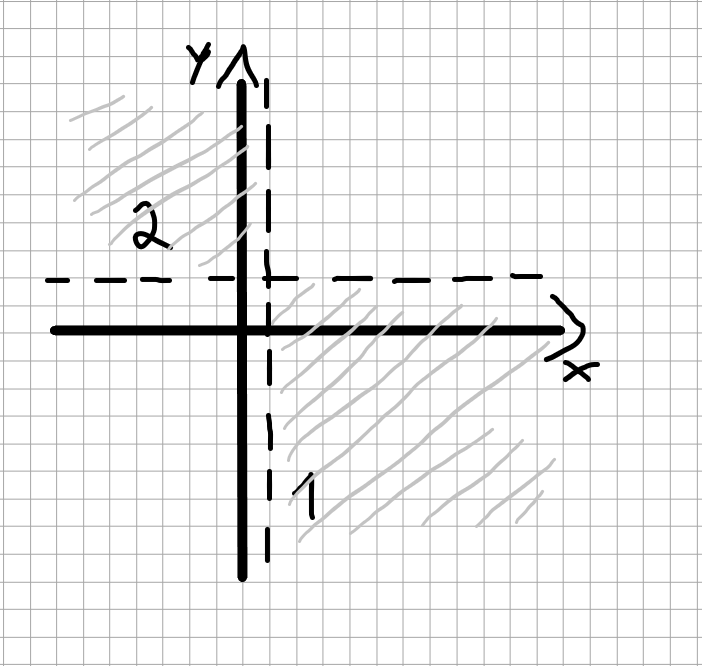
c)

2.uzdevums
Par funkciju y = f(x), kur x ∈ R, zināms, ka funkcija ir pāra un periodiska ar periodu 6, turklāt f(1) = 1, f(2) = 2.
a) Nosaki f(43); f(10) mun f(k + 5) – f(k – 1), k ∈ N. Pamato ar aprēķiniem vai spriedumiem.
b) Izvērtē un pamato, vai iespējams noteikt f(3) .

a) f(43) = f(7 * 6 + 1) = f(1) = 1
f(10) = f(-2 + 6 * 2) = f(-2) = f(2) = 2
f(k + 5) = f(k + 5 – 6) = f(k – 1)
f(k + 5) – f(k – 1) = 0

b) f(3) nav iespējams noteikt, jo zināma ir tikai informācija par:
f(1 + 6n)
f(2 + 6n)
f(-1 + 6n)
f(-2 + 6n), n ∈ Z

3.uzdevums
Nosaki visus izliektos četrstūrus, kuriem piemīt īpašība – visu četru iekšējo leņķu sinusi ir vienādi savā starpā. Pamato, ka citu četrstūru ar šādu īpašību nav.
Piezīme. Izliekta četrstūra katrs iekšējais leņķis ir mazāks nekā 180°.

-Leņķiem, kuri ir mazāki nekā 180°, leņķu sinusi ir vienādi, ja sina = sin(180° – a).

Apskatām iespējamos gadījumus:

• visi leņķi ir vienādi. Tie ir taisnstūri, tai skaitā kvadrāti.
• trīs leņķi ir vienādi

a + a + a + 180° – a = 360°
2a = 180°
a = 90° Iegūstam iepriekšējo gadījumu.

• divi leņķi savā starpā ir vienādi

-tie var būt pretēji leņķi, tad visi tie ir paralelogrami
-tie var būt vienas malaspieleņķi;
vienai malai tie ir a, a, un pretējai malai 180° – a.

Tātad tās ir vienādsānu trapeces. Citu gadījumu nav.