2.DAĻA

1.uzdevums
Atrisini nevienādību.

---

 

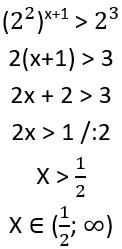
2.uzdevums
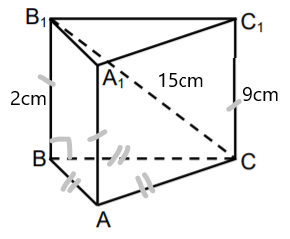
Regulāras trijstūra prizmasaugstuma garums ir 9 cm, bet sānu skaldnes diagonāles garums ir 15 cm. Aprēķini prizmas pamata šķautnes BC garumu un prizmas pilnas virsmas laukumu.

---

 

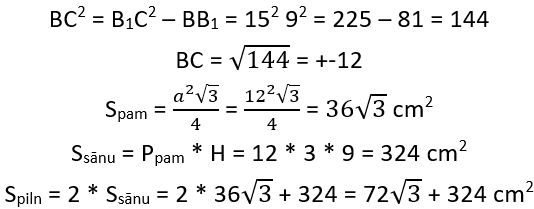
3.uzdevums
Atrisini vienādojumu .

---

 

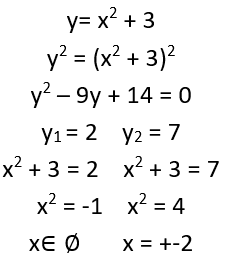
4.uzdevums
Dota izteiksmevisām pieļaujamām a vērtībām. Pārveido doto izteiksmi par daļu, savelc līdzīgos saskaitāmos iegūtās daļas skaitītājā un saīsini daļu.

---

 

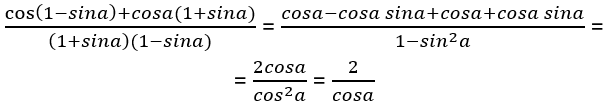
5.uzdevums
Dots funkcijas y = 6 – x grafiks.
a) Dotajā koordinātu plaknē uzzīmē funkcijasgrafiku. Zīmējot grafiku, nosaki koordinātas vismaz četriem grafika punktiem un atliec tos.
b) Izmantojot funkciju grafikus, nosaki vienādojumasakni.
c) Atrisini nevienādībuizmantojot funkciju grafikus.

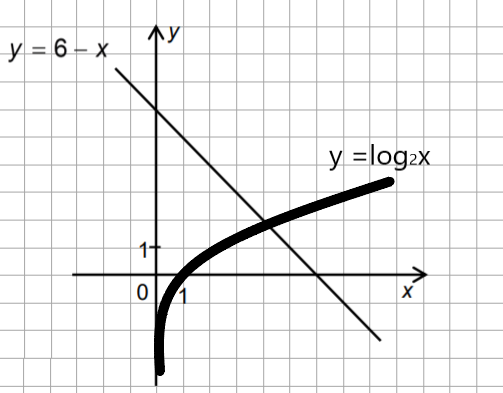
b) x = 4

c)

---

 

6.uzdevums
Atrisini nevienādību .

---

---

 

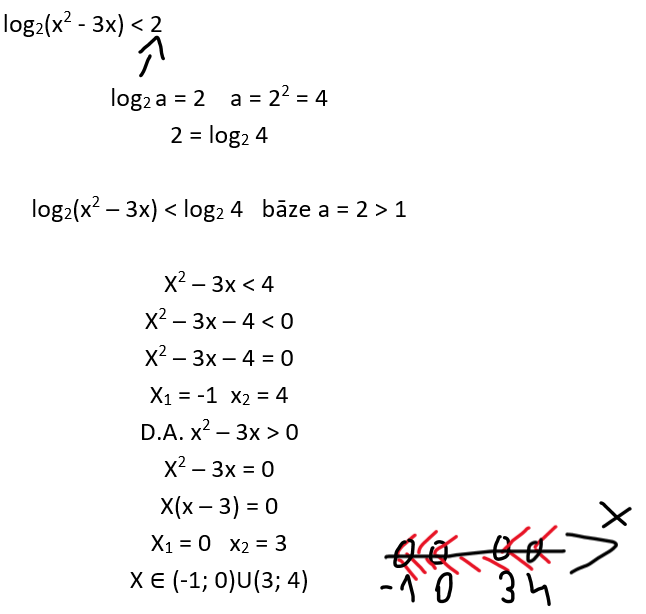
7.uzdevums
Par trijstūri ABC zināms, ka AB = 2 cm un AC = 6 cm, bet trijstūra ABC laukums ir . Aprēķini leņķa A iespējamās vērtības.

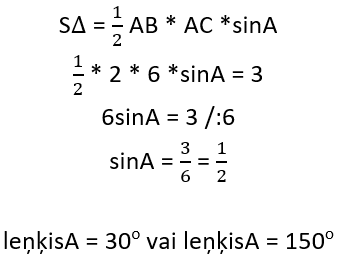
Atbilde: leņķis A = 30 grādi vai 150 grādi.

---

 

8.uzdevums
Skolas komanda piedalījās sacensībās un ieguva 73 punktus no 80 iespējamiem. Sacensības noritēja divās kārtās. Sacensību pirmajā kārtā komanda ieguva 95% no šajā kārtā iespējamo punktu skaita, bet otrajā kārtā – 90% no tajā iespējamo punktu skaita. Cik punktu skolas komanda ieguva pirmajā kārtā?

x…tik punktus varēja iegūt 1.kārtā

80 – x….tik punktus varēja iegūt 2.kārtā

0,95x + 0,9 (80 – x) = 73

0,95 + 72 – 0,9x = 73

0,05x = 1 /:20

x = 20 punktus (max punkti)

95% no 20 = 19 punktus ieguva 1.kārtā

---

 

9.uzdevums
a) Cik ir dažādu trīsciparu skaitļu, kuru pierakstā izmantoti tikai nepāra cipari (1; 3; 5; 7; 9)? Cipari skaitļa pierakstā var atkārtoties.
b) Uzraksti skaitlisku izteiksmi, kas izsaka, cik ir dažādu četrciparu skaitļu, kuru pierakstā ir trīs nepāra cipari un viens pāra cipars (0; 2; 4; 6; 8). Cipari skaitļa pierakstā var atkārtoties.

a) 5 * 5 * 5 = 125 skaitļi

---

 

10.uzdevums
Piramīdas SABC pamatā ir vienādsānu taisnleņķa trijstūris ABC (leņķis A = 90°). Piramīdas sānu šķautnes ir vienāda garuma un to garums ir 2a. Katra sānu šķautne ar pamata plakni veido 60° leņķi.
a) Nosaki, kur atrodas piramīdas augstuma pamats O, un papildini zīmējumu, uzzīmējot piramīdas augstumu SO.
b) Aprēķini piramīdas tilpumu.

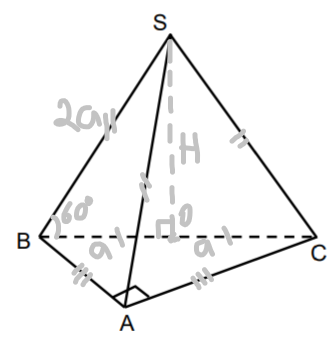
a) O atrodas pamata ABC apvilktas R.l. centrā, jo sānu šķautņu projekcijas ir vienāda garuma ( BO = OC = OA) uz hipotenūzas BC viduspunktā

---