3.DAĻA

1.uzdevums
Tilta margu veidošanai izmanto vienāda garuma tērauda stieņus, kas tiek sastiprināti tā, kā attēlots zīmējumā. Katra stieņa garums ir 3 metri.
a) Nosaki un pamato, vai ar 316 stieņiem pietiks, lai izveidotu margas, kuru garums (sk. zīm.) ir 240 metri.
b) Nosaki un pamato stieņu skaitu s, ja zināms, ka margu garums ir b metri (b∈N; b dalās ar 3).

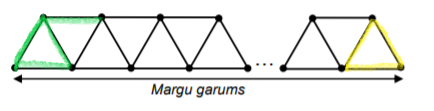
a) Tilta konstrukcijā atkārtojas ar zaļo krāsuizceltā figūra, kuras izveidei vajadzīgi 4 stieņi.
Ja tilta garums ir 240 m, tad kopā ir (240-3)/3 = 79 šādas figūras un viens vienādmalu trijstūris.
Kopā vajadzēs 79 * 4 + 3 = 319 stieņus > 316
Atbilde: nepietiks

b) Līdzīgā veidā būtu zaļās figūras, tādēļ stieņu skaits:
Atbilde:

2.uzdevums
Caur taisnstūra ABCD diagonāļu krustpunktu O novilkta taisne, kas perpendikulāra diagonālei BD un krusto taisnstūra malas BC un AD attiecīgi punktos E un F (sk. att.). Pierādi, ka
a) trijstūris BEO ir vienāds ar trijstūri DFO,
b) DB ir leņķa EDA bisektrise,
c) trijstūru BED un FED laukumi ir vienādi.

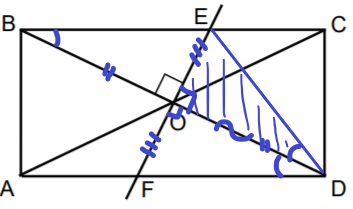
a) BO = OD, jo taisnstūra diagonāles krustojoties dalās uz pusēm.
leņķis DOF = leņķi BOE = 90°(krustleņķi)
leņķis EBO = leņķi ODF (šķērsleņķi)
pēc pazīmes lml trijstūris BEO = trijstūri DFO

b) no trijstūra vienādības => EO = OF
pēc pazīmes mlm ( OD – kopīga mala)
trijstūris EOD = trijstūriFOD => leņķis EDO = leņķi FDO => BD – leņķa EDA bisektrise

c)

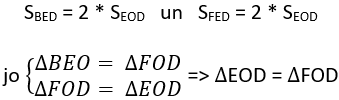
3.uzdevums
Doti vienādojumi 1 + cos4x = 0 un Nosaki vienu tādu x ∈ [π; 2π], kas ir sakne abiem dotajiem vienādojumiem, un vienu tādu x∈[π; 2π], kas ir sakne tikai vienam no dotajiem vienādojumiem.

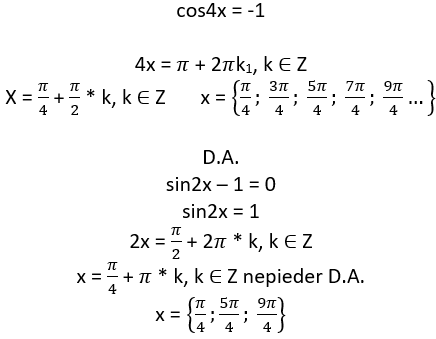
Abu vienādojumu atrisinājumi ir .

Tikai pirmāvienādojuma atrisinājums ir .