2.DAĻA
1.uzdevums
Atrisini vienādojumu 
.
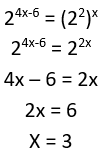
2.uzdevums
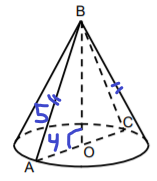
Konusa aksiālšķēlums ir trijstūris ABC, kura malu garumi ir 5 cm, 5 cm, 8 cm. Aprēķini konusa pamata rādiusa AO garumu, konusa augstuma BO garumu un konusa tilpumu.
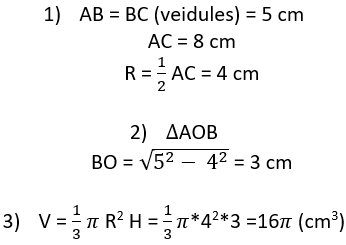
3.uzdevums
Atrisini nevienādību 
.
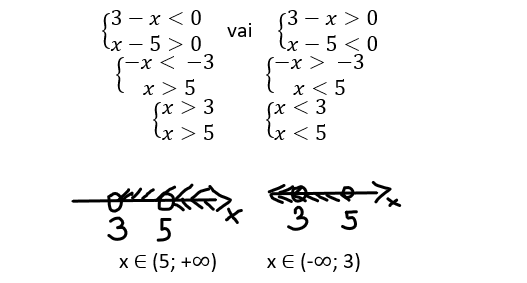
Atbilde: x ∈ (-∞; 3) U (5; +∞)
4.uzdevums
Dota izteiksme
, kur x ≠ 0 un x ≠ 1. Izpildi darbības:
– izteiksmi iekavās pārveido par daļu un iegūtās daļas skaitītājā savelc līdzīgos saskaitāmos;
– sareizini daļas un reizinājumā iegūto daļu saīsini.
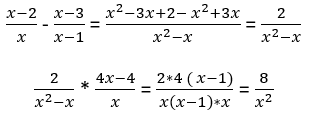
5.uzdevums
Atridini vienādojumu 
.
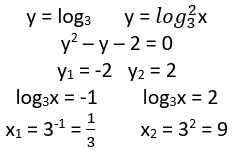
6.uzdevums
Pēc izņemšanas no krāsns maizes klaips 4 stundas tika atdzesēts istabas temperatūrā. Šajā laikā klaipa temperatūru T Celsija grādos atkarībā no laika t stundās izsaka funkcija T(t) = 20 + 160 * 
,kur t∈[0;4].
a) Aprēķini klaipa temperatūru pēc pilnām 3 stundām, kopš tas tika izņemts no krāsns.
b) Par cik grādiem samazinājās klaipa temperatūra 4 stundu laikā, kopš tā izņemšanas no krāsns?
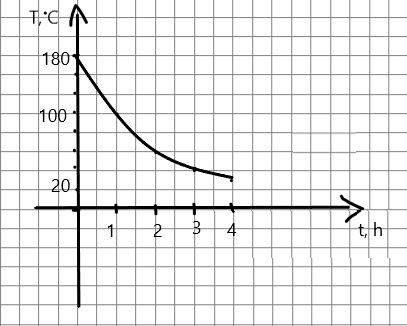
c) Izveido koordinātu plakni un uzzīmē grafiku funkcijai T(t) = 20 + 160 * ,kur t∈[0;4].
d) No grafika nosaki vai aprēķini, kuras stundas (pirmās, otrās, trešās, ceturtās) laikā klaipa temperatūra samazinājās visstraujāk?
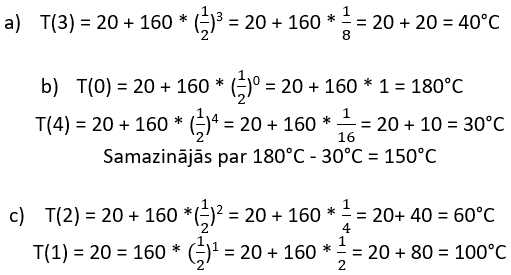
d) Pirmās stundas laikā (par 80°).
7.uzdevums
Mazjaudas motociklu numura zīmēs simboli tiek izvietoti divās rindās (sk. paraugus). Pirmajā rindā ir divi burti. Izmantojamie 22 burtu simboli ir A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, R, S, T, U, V, Z.
Otrajā rindā ir no viena līdz trim cipariem, kas veido skaitļus no 1 (ieskaitot) līdz 999 (ieskaitot).
a) Cik dažādu numura zīmju, kuru pirmā rinda ir „AA”, var izveidot?
b) Cik dažādu numura zīmju, kuru otrā rinda ir „5”, var izveidot?
c) Uzraksti skaitlisku izteiksmi, kas izsaka, cik pavisam kopā dažādu numura zīmju var izveidot.
a) 999 numura zīmes
b) 22 * 22 = 484 zīmes
c) 484 * 999
8.uzdevums
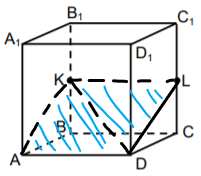
Dots kubs ABCDA1B1C1D1 (sk. att.). Punkti K un L ir attiecīgi šķautņu BB1 un CC1 viduspunkti.
a) Nosaki leņķa ADL lielumu grādos un pamato to.
b) Uzzīmē dotā kuba šķēlumu ar plakni ADL. Pieraksti iegūto šķēlumu, norādot tā virsotnes.
c) Nosaki taišņu KD un AC1 savstarpējo novietojumu (paralēlas, krustiskas, šķērsas).
b) ADLK
c) šķērsas
9.uzdevums
Taisnas trijstūra prizmas ABCA1B1C1 pamatā ir vienādsānu taisnleņķa trijstūris (leņķis ABC = 90°), kura katešu garums ir a
. Garākā sānu skaldnes diagonāle ar pamata plakni veido 60° leņķi.
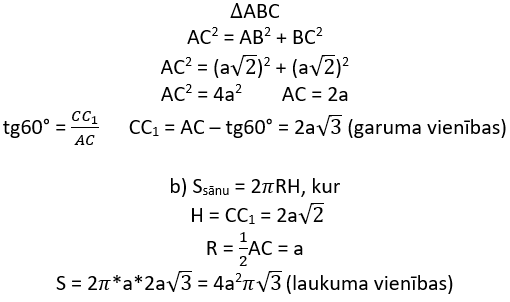
a) Aprēķini prizmas augstumu.
b) Aprēķini prizmai apvilktā cilindra sānu virsmas laukumu.
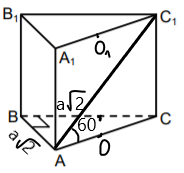
a) garākā sānu skaldnes diagonāle ir AC, jo tā balstās uz garāko projekciju ( AC>BC, jo AC ir hipotenūza)
10.uzdevums
Pircējs nolēma iegādāties divas grāmatas. Vienai grāmatai bija 10% atlaide, bet otrai grāmatai bija 20% atlaide. Izsakot eiro, abas atlaides bija vienādas. Pircējs par abām grāmatām kopā samaksāja 26 eiro. Cik eiro pircējs samaksāja par katru no grāmatām?
x…tik maksā viena grāmata
y…tik maksā otra gramata
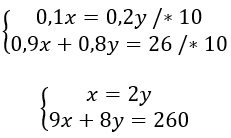
9 * 2y + 8y = 260
26y = 260
y = 10 eiro (bez atlaides)
0,8y = 8 eiro
x = 2y = 20 eiro
0,9x = 18 eiro
Atbilde: par pirmo gratamu samaksāja 18 eiro, par otru 8 eiro.