Logaritmiskā funkcija

Tā kā , tad katram skaitlim  eksistē tikai viens vienīgs kāpinātājs , kurā kāpinot skaitli  iegūst . Piemēram,, jo tikai , Taču mūs var interesēt arī atbilde uz jautājumu, kādā pakāpē jākāpina viena noteikta bāze , lai iegūtu jebkuru pozitīvu skaitli.

Definīcija.

Par logaritmisko funkciju sauc funkciju , kas katram pozitīvam skaitlim piekārto tā logaritmu (kāpinātāju) pie dotās bāzes .

Piemēram, logaritmiskās funkcijas ir 
Tākā logaritma bāze tad  pakāpes var būt tikai pozitīvi skaitļi,
tas ir, ja 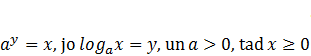. Tāpēc logaritmiskā funkcija  ir definēta tikai pozitīvām argumenta  vērtībām un 

Logaritmiskās funkcijas vērtība var būt jebkurš reāls skaitlis, tāpēc

Logaritmiskās funkcijas 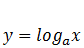īpašības

Grafiks un krustpunkti ar asīm

Logaritmiskās funkcijas grafiku iegūst, sastādot atbilstošu vērtību tabulu un iegūtos punktus atliekot koordinātu plaknē. Tā kā logaritmiskās funkcijas definīcijas apgabals ir , tad funkcijas grafiks  asi nekrusto un vienmēr atrodas no tās pa labi.
Noteiksim krustpunktu ar asi: lai to izdarītu, aprēķina funkcijas vērtību punktā Y = 0. Ja Y = 0, tad un 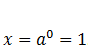. Šādu vērtību iegūst neatkarīgi no parametra  vērtības.

Secinājums.

Logaritmiskās funkcijas grafiks krusto 0x asi punktā (1;0) visām a vērtībām.

Logaritmiskās funkcijas monotonitāte

Līdzīgi kā eksponentfunkcijai 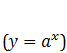, arī logaritmiskajai funkcijas augšana vai dilšana ir atkarīga no bāzes a vērtības.
Ja a > 1, tad logaritmiskā funkcija aug visā definīcijas apgabalā.
Piemēram, funkcijas ir augošas.

Ja a < 0, tad logaritmiskā funkcija dilst visā definīcijas apgabalā.
Piemēram, funkcijas 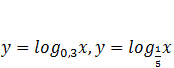ir dilstošas.

Zinot logaritmiskās funkcijas monotonitātes īpašības, viegli salīdzināt dažādu logaritmu vērtības, ja to bāzes ir vienādas . Piemēram: 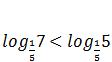jo funkcija 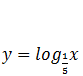dilstoša un lielākai argumenta vērtībai atbilst mazāka funkcijas vērtība.
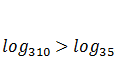, jo funkcija 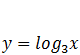ir augoša un lielākai argumenta vērtībai atbilst lielāka funkcijas vērtība.

Logaritmiskās funkcijas vienādzīmju intervāli, min un max vērtības.

Ņemot vērā šīs divas īpašības un funkcijas vērtību apgabalu, secinām, ka logaritmiskajai funkcijas neeksistē ne lielākā, ne mazākā vērtība.

Logaritmiskā funkcija nav periodiska, un nav ne pāra, ne nepārafunkcija.